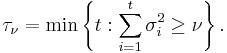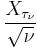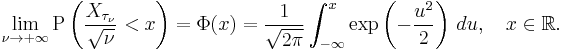Martingale central limit theorem
In probability theory, the central limit theorem says that, under certain conditions, the sum of many independent identically-distributed random variables, when scaled appropriately, converges in distribution to a standard normal distribution. The martingale central limit theorem generalizes this result for random variables to martingales, which are stochastic processes where the change in the value of the process from time t to time t + 1 has expectation zero, even conditioned on previous outcomes.
Statement
Here is a simple version of the martingale central limit theorem: Let
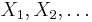 -- be a martingale with bounded increments, i.e., suppose
-- be a martingale with bounded increments, i.e., suppose
and
almost surely for some fixed bound k and all t. Also assume that 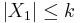 almost surely.
almost surely.
Define
and let
Then
converges in distribution to the normal distribution with mean 0 and variance 1 as 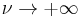 . More explicitly,
. More explicitly,
References
Many other variants on the martingale central limit theorem can be found in:
- Hall, Peter; and C. C. Heyde (1980). Martingale Limit Theory and Its Application. New York: Academic Press. ISBN 0-12-319350-8.
- For the discussion of Theorem 5.4 there, and correct form of Corollary 5.3(ii), see Bradley, Richard (1988). "On some results of MI Gordin: a clarification of a misunderstanding". Journal of Theoretical Probability (Springer) 1 (2): 115–119. doi:10.1007/BF01046930.
![\operatorname{E}[X_{t%2B1} - X_t \vert X_1,\dots, X_t]=0\,,](/2012-wikipedia_en_all_nopic_01_2012/I/a090a8df6437772dd7c2cdef518dc31b.png)
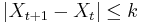
![\sigma_t^2 = \operatorname{E}[(X_{t%2B1}-X_t)^2|X_1, \ldots, X_t],](/2012-wikipedia_en_all_nopic_01_2012/I/ce478d1f96aa30870a064ee2811eb961.png)